モンテカルロ法

円周率

---

よく例として使われるのがモンテカルロ法を使って円周率を出す方法があるので、 ここでも従ってみる。

モンテカルロ法では乱数が重要となっている。

乱数はある範囲から無差別に拾ってきた数字という意味で、こういった確率のシミュレーションには必須のものである。

しかしコンピューターの中では完全な乱数(出てきた数字が何にも依存しない)というのはほぼ無理なので、擬似乱数というものを使う。 疑似乱数はseed値というものが必要で、seed値を元に乱数を作る。疑似乱数の中身はここでは詳しく扱わない。

まずは、サンプルコードを載せる。

#include <iostream>
#include <random>
    
int main(int argc, char *argv[]) {
  int iSeed = 0;
  int nAll = 1e+8;
  int nInside = 0;
  if (argc != 3) {
    std::cerr << "Please input [seed number] [number of trials]" << std::endl;
    return 1; 
  }
  iSeed=std::atoi(argv[1]);
  nAll=std::strtod(argv[2], NULL);
  std::cout << "seed number: " << iSeed << ", trial number: " << nAll << std::endl;
  double rCircle=1.0, xyMin=0.0, xyMax=1.0;
  std::mt19937_64 engine(iSeed);
  std::uniform_real_distribution<double> uniformRand(xyMin, xyMax);
  double xRand = 0.0, yRand = 0.0, eval = 0.0;
  for (int i = 0; i < nAll; ++i) {
    xRand=uniformRand(engine);
    yRand=uniformRand(engine);
    eval=sqrt(pow(xRand, 2) + pow(yRand, 2));
    if (eval < rCircle) nInside +=1;
  }
  double insideRate=(double)nInside / (double)nAll;
  std::cout << insideRate << std::endl;
  std::cout << insideRate * 4 << std::endl; // 4等分の円なので、4倍
  return 0;
}

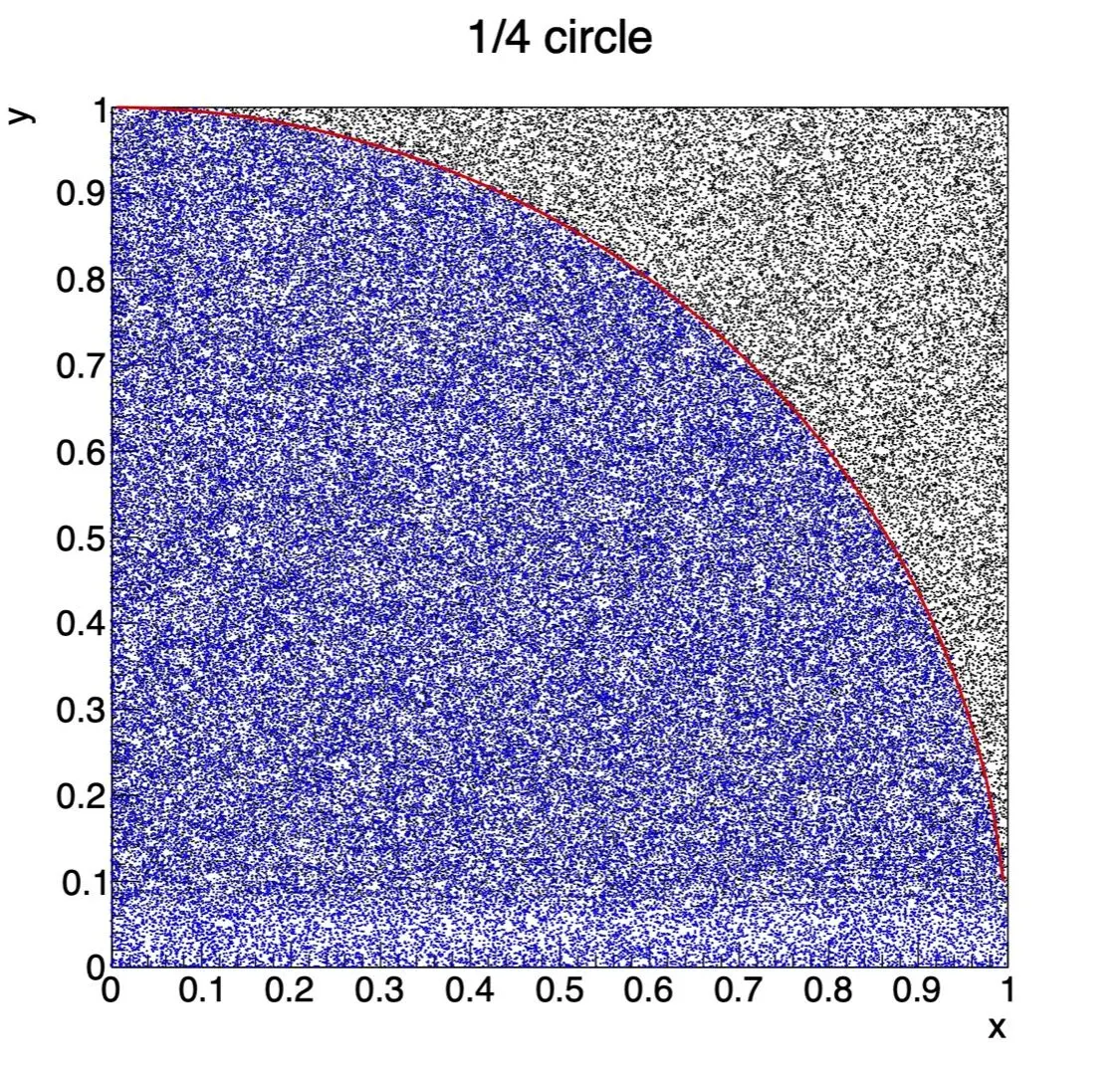
このプログラムでは、図1に示すように1 x 1の正方形の中に半径1の円を描いて正方形の中でランダムに点描をしたとき、 円の内側に入った点の確率を求めるということをしている。

これは正方形の中に均等に点をうった場合、円の内側に入る確率は単純に(円の面積)/(正方形の面積)となる。 今回の場合は、正方形の面積は1 x 1 = 1、円の面積は 1^2 * π=πで、今回は1/4の円なので面積はπ/4。 つまり、(円の面積)/(正方形の面積) = (π/4) / 1 = π/4となり、円周率を計算する場合はこれを4倍すればいいことがわかる。